Como é que se mede a altura das montanhas?

Durante milhares de anos, diferentes métodos foram utilizados para tentar calcular a altura das montanhas do nosso planeta. O que são e como isso é feito atualmente? Nós explicamos para você aqui.

Altura montanhas
Medir com exatidão a altura das montanhas tem sido uma das tarefas mais complicadas que a humanidade já enfrentou. Como é que isso é feito hoje em dia?

O ser humano sempre teve um fascínio em descobrir os segredos dos lugares mais inacessíveis do planeta. Um deles é a altura das montanhas, objeto de lendas ou suposi��ões em culturas antigas, que consideravam que os picos mais altos eram habitados pelas suas divindades, sendo território proibido para a nossa espécie.

Quando é que os humanos começaram a perceber que era importante saber o tamanho de uma montanha? A resposta é complicada, mas sabe-se que as culturas antigas da China, do Oriente Médio, do Egito, algumas culturas pré-colombianas da América, ou os gregos e romanos dispunham de meios para medir a altura dos relevos.

As primeiras tentativas para calcular a altitude

Para isso, utilizaram as fórmulas trigonométricas dos triângulos retângulos que todos estudámos na escola ou no liceu: o seno, o cosseno e a tangente. Esta última é a mais importante, pois é o resultado da divisão do cateto oposto (a altura da montanha) pelo adjacente (a distância da base da montanha até à pessoa que mede a sua altura).

youtube video id=XckUBruPm-8

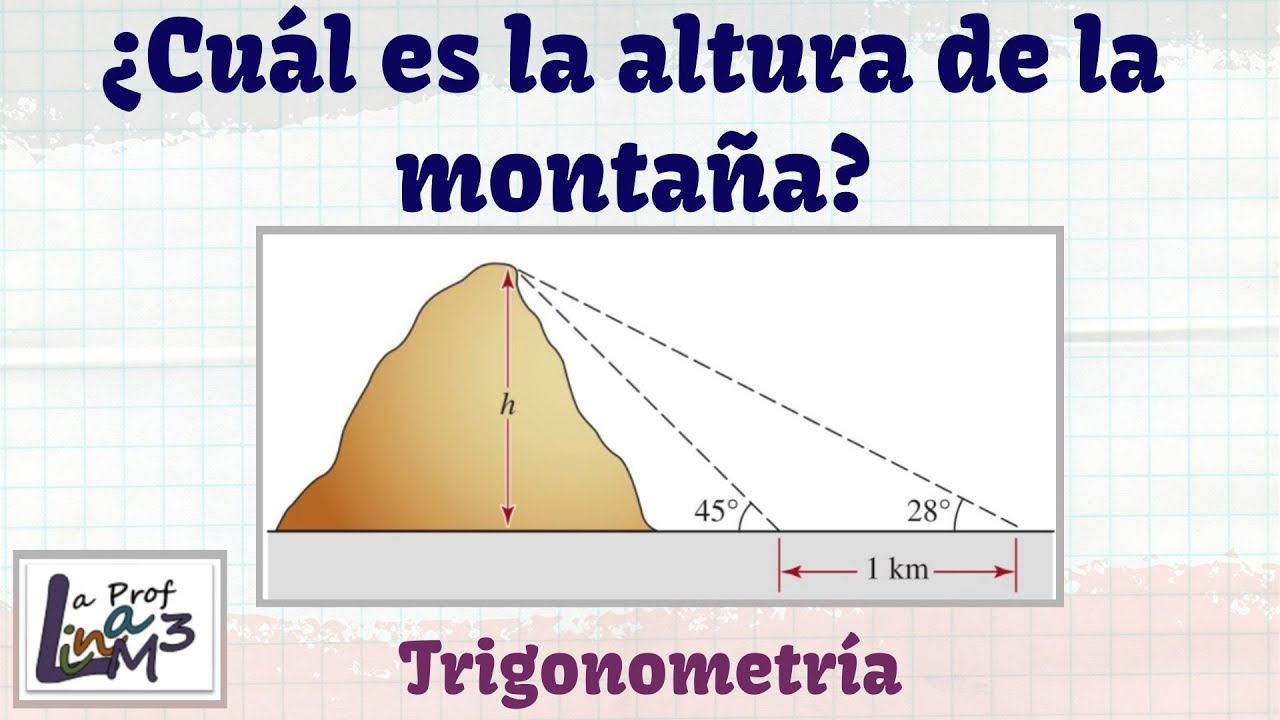
Graças a esta função, estas culturas antigas conseguiam obter a altura aproximada das montanhas. Além disso, utilizavam instrumentos de referência nos quais podiam anotar as unidades. A partir daí, não se registaram grandes desenvolvimentos durante muitos séculos, até que, no século XVII, se começou a utilizar as mudanças da pressão atmosférica.

As medições de Humboldt e Everest

E aqui entra em cena Alexander von Humboldt, o pai da Geografia moderna. Em 1802, mediu a altura do Chimborazo, no Equador. Para tal, utilizou um barômetro. Vale a pena recordar que este vulcão colossal é o ponto mais alto da Terra se tomarmos como ponto de referência o centro do planeta em vez do nível do mar.

Humboldt subiu ao cume e, utilizando as leis de Torricelli, que estabelecem que a pressão diminui com a altitude, não de forma totalmente linear, mas quase, conseguiu calcular a altura aproximada deste colosso. O problema deste método é que a variação das condições meteorológicas locais, que são ainda mais acentuadas em alta montanha, faz com que a pressão também varie, tornando-o numa técnica imprecisa.

Algumas décadas mais tarde, surgiu uma nova forma de medir a altura das montanhas graças aos teodolitos, instrumentos mecânicos e ópticos muito semelhantes a um telescópio, que permitiam medir com grande precisão os ângulos verticais e horizontais ao nível da rua. Um dos seus principais promotores foi George Everest, o topógrafo britânico que, nos anos 50, deu o seu nome à rainha das montanhas da Terra.

Conhecendo um dos lados do triângulo (a distância horizontal à montanha ou o cateto adjacente) e a tangente do ângulo, por trigonometria, pode calcular-se a altura da montanha (o cateto oposto). Mas este método também tinha problemas, pois quanto mais longe estivesse o sopé da montanha, mais impreciso seria o cálculo.

A altura é a distância vertical de um corpo à superfície da Terra ou ao solo, enquanto a altitude é a distância vertical ao nível do mar.

Outra desvantagem importante é o nível de referência: onde é que colocamos o 0? Não se deve esquecer que a altura é medida em relação a uma referência. Já se sabia que o nível do mar, que poderia ser a referência mais adequada, oscilava, e calculava-se uma média entre o nível máximo e o nível mínimo da maré para obter a altitude.

Além disso, também sabemos que a Terra não é uma esfera perfeita: é um elipsoide que é achatado nos pólos e mais largo no equador devido à rotação, algo que influencia as medidas das montanhas. E é por isso que, se medir a altura do Evereste em relação ao centro da Terra, é mais baixa do que a do Chimborazo. E para complicar ainda mais as coisas, o nível do mar varia cerca de 100 metros e é preciso ter em conta o efeito das marés.

É assim que se mede atualmente a altura das montanhas

Atualmente, as alturas das montanhas são calculadas por gravimetria. Ao medir a gravidade em diferentes pontos, pode saber a que altura teórica estaria o hipotético nível do mar, o geoide: esta é a superfície de referência para calcular a altura dos cumes das montanhas. É obtido a partir de triangulações de satélites GPS.

Estes sistemas requerem pelo menos três satélites para a medição da superfície e quatro para a medição da altura, calculando o tempo que o sinal demora a chegar ao satélite que efetua a medição e, a partir daí, é possível calcular a distância.

As técnicas, ainda atuais, mais precisas para medir a altura de um objeto terrestre são o LIDAR (Light Detection and Ranging), que emite um feixe de infravermelhos e calcula o tempo de atraso entre essa emissão e o sinal que é refletido ao "bater" no objeto que se pretende medir. De fato, esta técnica é hoje amplamente utilizada na cartografia para muitos outros fins.