O que uma equação de quase 190 anos atrás sobre tempestades nos pode dizer?

Decorria o ano de 1835 quando o engenheiro e físico francês Émile Clapeyron descobriu porque as menores pressões em altitude afetam o ponto de ebulição da água, de forma que esta ferve mais rapidamente sob uma temperatura menor.

O seu trabalho estabeleceu a relação entre a pressão de uma substância e a temperatura, quando duas fases dessa substância se encontram em equilíbrio. Essa relação é conhecida hoje como a equação de Clausius-Clapeyron.

O impacto desta equação atualmente

Quase 200 anos depois, esta relação ajuda os meteorologistas a compreender os efeitos das mudanças climáticas. A equação mostra como o ar mais quente pode conter mais umidade, que é crucial para prever o aumento de tempestades e a maior intensidade da precipitação.

"Um ponto chave sobre esta equação é que ela tem um exponencial lá dentro", diz Peter Stott, climatologista do Gabinete Britânico de Meteorologia. "Uma curva exponencial, é claro, quanto mais sobe mais se acentuada. Então, à medida que a temperatura aumenta, o nível de precipitação acompanha este aumento".

Portanto, a equação aponta para um futuro com mais umidade e, como os pesquisadores começaram a notar, isto é apenas o início. As tempestades no futuro podem produzir ainda mais chuvas do que a equação prevê.

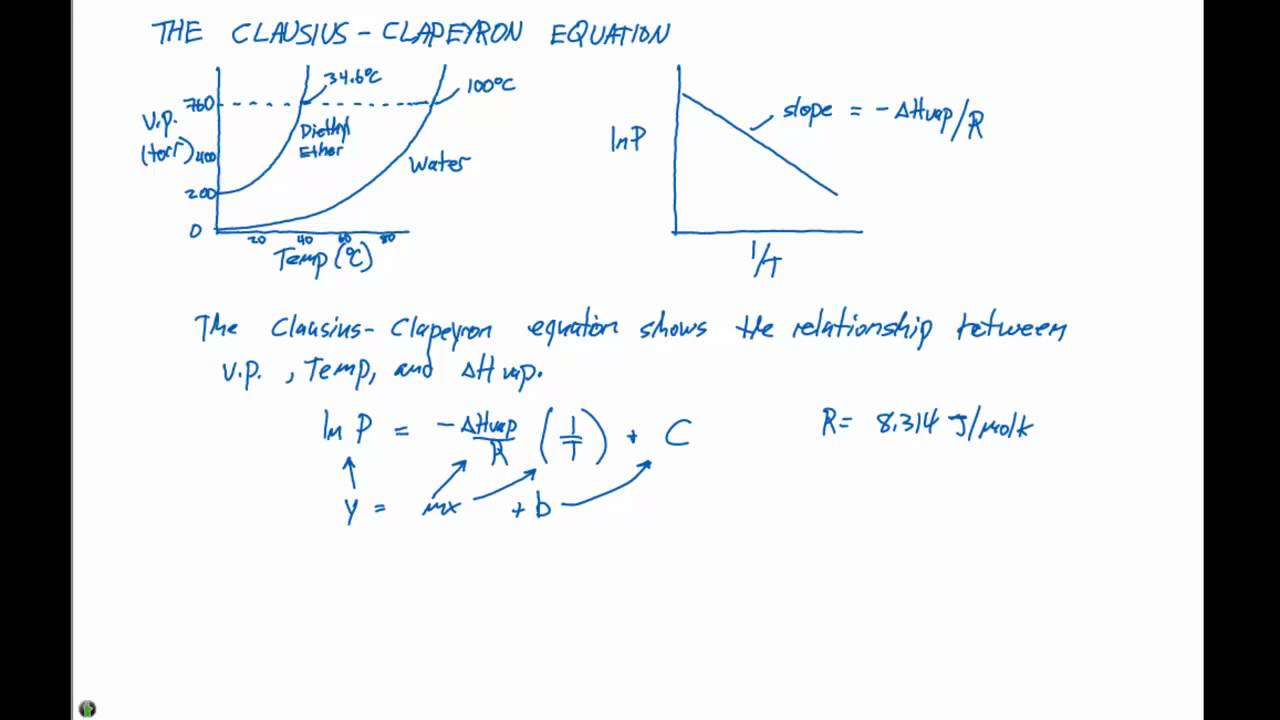
A equação de Clausius-Clapeyron

Era a época da máquina a vapor. Um grupo de cientistas composto por Sadi Carnot, James Joule, William Rankine e William Thomson, assim como Émile Clapeyron e Rudolf Clausius, trabalharam na teoria e aplicações práticas para tentar melhorar a eficiência desta tecnologia crucial a vapor.

Clapeyron foi um dos primeiros a considerar a teoria de como os estados gasoso e líquido da água se comportam enquanto este fluido é aquecido dentro de uma máquina a vapor. Em 1834, ele tinha teorizado de que forma a pressão do vapor - que é a pressão exercida pelo vapor quando em equilíbrio com o líquido - poderia mudar com a temperatura.

Em 1850, Clausius refinou a relação incluindo o calor latente, que é a quantidade de calor que cada grama de substância precisa receber ou perder para que a mudança de estado seja possível. Isso deu a forma da equação que é usada hoje.

Esta equação pode explicar observações diárias, como, por exemplo, uma panela de pressão poder aquecer a água mais rapidamente ao fervê-la a 120°C. Cientistas de várias áreas utilizam esta equação, calculando desde a composição provável de atmosferas e oceanos de outros planetas, até ao potencial energético.

Contudo, uma das suas aplicações mais importantes é na meteorologia, particularmente em simulações de como a atmosfera e o clima irão responder às mudanças climáticas.

Os meteorologistas utilizam a equação de Clausius-Clapeyron para compreender em que momento o vapor d'água se condensará para o estado líquido. Isto acontece devido à pressão de vapor de saturação, que é a pressão máxima que pode ser exercida pelo vapor d'água antes de se condensar. A equação mostra que esta pressão aumenta exponencialmente com a temperatura.

A equação mostra que para cada grau Celsius extra de aquecimento, o ar pode conter mais 7% de água. Dessa forma, com um aumento de 2°C do aquecimento global, o mundo poderia esperar mais 14% de umidade no ar, e com 3°C de aquecimento, esse valor seria de 21%, e assim sucessivamente.

As tempestades de hoje

Grande parte das fortes chuvas e inundações observadas na Califórnia nos últimos meses e anos, tiveram origem em eventos que começaram sobre o oceano, que transportaram a quantidade total de vapor d'água extra, prevista pela equação de Clausius-Clapeyron.

Estas tempestades são impulsionadas pelo deslocamento de longos e estreitos corredores de vapor d'água, chamadas de rios atmosféricos, que muitas vezes têm origem nos trópicos.

"O aumento global da temperatura está mais próximo de 1,2 °C, então há, provavelmente, 8% mais umidade nos rios atmosféricos hoje do que teria se não houvesse mudanças climáticas", diz Stott.

Porém, às vezes o aumento da precipitação é menor do que o previsto pela equação, devido a um aspecto físico pouco compreendido pela microfísica de nuvens, o chamado eficiência da precipitação.

Em resumo, nem todo o vapor d'água condensado do ar chega, de fato, ao solo como chuva ou neve, pois parte dele evapora de novo.