Pesquisadores definem equação universal para o bater de asas. Ela pode ser aplicada aos seres humanos?

A capacidade de voar e a energia necessária para fazer isso não tinham sido definidas, até agora. A nova fórmula matemática é comum a todas as espécies animais que batem as asas.

voo, aves, pássaros
Uma equação universal descreve o bater de asas.

Assim como os diferentes grupos de animais evoluíram ao longo da sua história, a capacidade de voar também evoluiu de forma independente em cada um destes grupos de animais.

Os biólogos responsáveis por esta pesquisa esperavam que houvesse um padrão na frequência com que os animais batem as asas. O desafio era encontrar uma expressão matemática que descrevesse esse processo de uma forma comum a todas as espécies.

Pesquisadores da Universidade de Roskilde, na Dinamarca, apresentaram uma equação universal que descreve a frequência do batimento de asas em pássaros, insetos e morcegos.

Por que definir a frequência no bater de asas?

Qualquer animal voador procurará minimizar a energia necessária para realizar o seu voo permanecendo no ar. Para fazer isso, você deve encontrar uma frequência ideal no movimento da batida das asas.

Frequência é a medida do número de vezes que um fenômeno ou processo periódico se repete por unidade de tempo.

Esta frequência dependerá da massa do animal e da área da asa. Desta forma, o peso de cada animal e a área da superfície de sua asa são os dois princípios desta fórmula universal.

Segundo seus autores, não existe uma fórmula mais simples e fisicamente significativa que possa descrever a frequência de “bater as asas” em animais voadores ou nadadores.

Qual é a fórmula e por que é tão simples?

A essência desta fórmula deriva de princípios físicos básicos e é definida como: a frequência do batimento das asas (f) é proporcional à raiz quadrada da massa corporal (m) do animal dividida pela área (A) da sua asa ou barbatana.

Além disso, se forem feitos alguns ajustes a esta expressão matemática, ela também é válida para animais nadadores como baleias ou pinguins, apesar das suas diferenças de tamanho, história evolutiva e estruturas de asas ou natação.

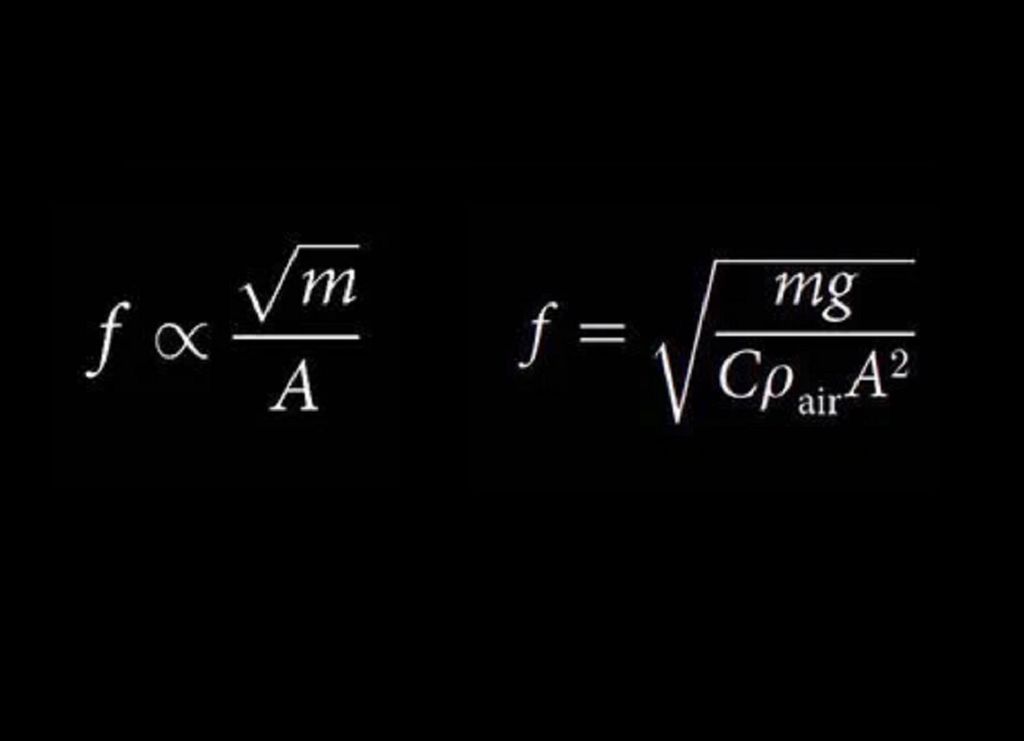
Equação da frequência da batida de asas
Versão simples da equação universal (esquerda) e fórmula completa (direita) Fonte: Jensen et al. (2024).

A versão completa da fórmula também inclui a intensidade do campo gravitacional (g), um valor adimensional denominado C, que descreve a forma, o movimento e outras características das asas, e a densidade do ar (ρ ar).

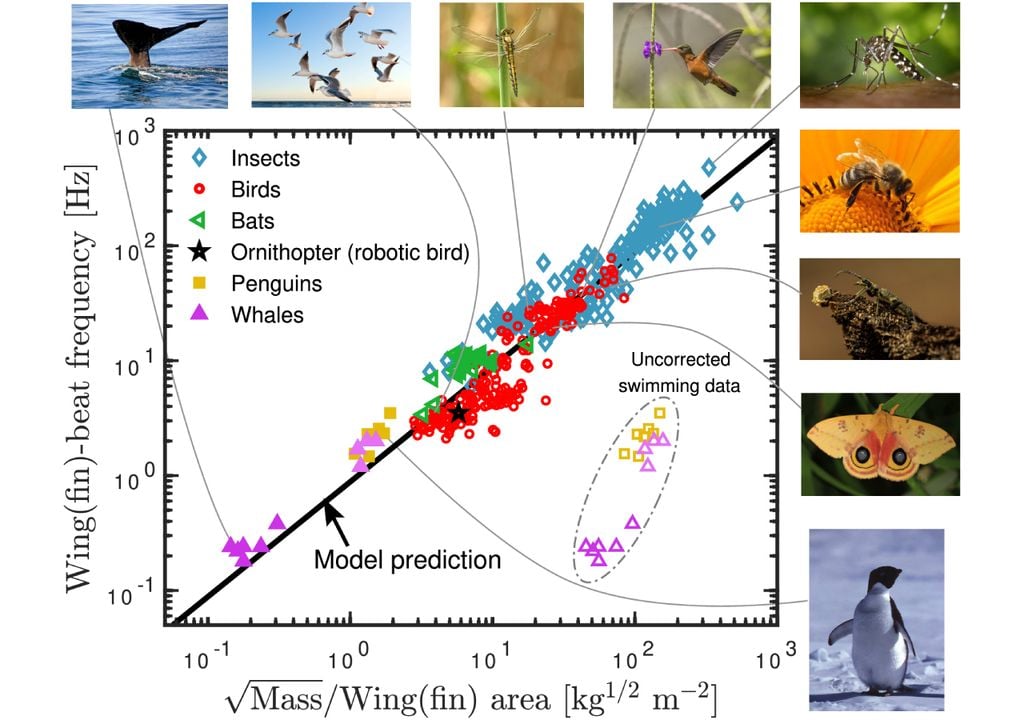
Os pesquisadores descobriram que todos os animais voadores seguem essa proporcionalidade com aproximadamente o mesmo coeficiente. E os animais nadadores também seguem a mesma relação universal ao corrigir a flutuabilidade e a diferença entre a densidade do ar e a densidade da água.

Mas como puderam comprovar?

Eles conseguiram verificar a precisão de sua equação em animais voadores com dados publicados sobre frequências de batimento de asas em abelhas, mariposas, libélulas, besouros, mosquitos, morcegos e pássaros de diferentes tamanhos.

Apesar de não encontrarem estudos com todas as informações necessárias para animais nadadores, eles reuniram dados para comparações e estimativas sobre as frequências de movimento das nadadeiras em pinguins e diversas espécies de baleias. E demonstraram que esta fórmula também é válida para animais mergulhadores com flutuabilidade positiva, que devem mover continuamente a água para cima para permanecerem submersos; e excluindo peixes pois estes ajustam sua flutuabilidade com uma bexiga natatória.

Gráfico de frequência do bater de asas
Resultados da frequência de bater de asas ou nadadeiras de vários animais. Fonte: Jensen et al. (2024).

Além disso, calcularam que o maior animal voador já conhecido, um pterossauro, era capaz de mover as suas asas de 10 metros quadrados a uma frequência de 0,7 hertz ou vezes por segundo.

No total, os resultados de 414 animais, desde grandes cetáceos a pequenos insetos voadores, diferem por quase um fator de 10.000 na frequência do bater das asas ou das nadadeiras. No entanto, essas frequências caem na mesma linha do gráfico que representaram.

Esta fórmula é aplicável a espécies não voadoras ou nadadoras?

Embora a fórmula não seja proposta para animais não voadores ou nadadores, eles também consideram o exemplo de como ela seria aplicada à espécie humana.

Se uma pessoa pesa 70 kg e constrói asas com uma área total de 2 metros quadrados, ela precisaria batê-las cerca de 4 vezes por segundo para permanecer no ar.

Portanto, embora a equação não exclua isso, se movimentarmos os braços podemos perceber que isso é muito difícil e concluir que o ser humano não foi feito para voar.

Segundo os pesquisadores, no caso de animais extremamente pequenos a equação seria limitada pela dinâmica dos fluidos. A equação é a mesma, mas sem raiz quadrada para animais menores que um inseto de tamanho médio. Isto poderia ter implicações para o desenvolvimento de futuros nanorrobôs voadores, ou robôs nanoscópicos aproximadamente do tamanho de um átomo.

Referência da notícia:

Jensen, J. H.; Dyre, J. C.; Hecksher, T. Universal wing- and fin-beat frequency scaling. PLoS ONE, 19(6), 2024.